二分类器及其性能指标

了解数据集
训练一个二分类器
性能指标分析
多类分类器
误差分析
多输出分类器

手写数字识别数据集可视化

import pandas as pd
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline

train_set = pd.read_csv("../Dataset/digit-recognizer/train.csv")
test_set = pd.read_csv("../Dataset/digit-recognizer/test.csv")
print(train_set.head())
print("*"*40)
print(train_set.info())

       label  pixel0  pixel1  pixel2  pixel3  pixel4  pixel5  pixel6  pixel7  \
    0      1       0       0       0       0       0       0       0       0
    1      0       0       0       0       0       0       0       0       0
    2      1       0       0       0       0       0       0       0       0
    3      4       0       0       0       0       0       0       0       0
    4      0       0       0       0       0       0       0       0       0

       pixel8    ...     pixel774  pixel775  pixel776  pixel777  pixel778  \
    0       0    ...            0         0         0         0         0
    1       0    ...            0         0         0         0         0
    2       0    ...            0         0         0         0         0
    3       0    ...            0         0         0         0         0
    4       0    ...            0         0         0         0         0

       pixel779  pixel780  pixel781  pixel782  pixel783
    0         0         0         0         0         0
    1         0         0         0         0         0
    2         0         0         0         0         0
    3         0         0         0         0         0
    4         0         0         0         0         0

    [5 rows x 785 columns]
    ****************************************
    <class 'pandas.core.frame.DataFrame'>
    RangeIndex: 42000 entries, 0 to 41999
    Columns: 785 entries, label to pixel783
    dtypes: int64(785)
    memory usage: 251.5 MB
    None

def plot_digit(data):
    image = data.reshape(28,28)
    plt.imshow(image, cmap = matplotlib.cm.binary,interpolation="nearest")
    plt.axis("off")

plot_digit(train_set.iloc[1,1:].values)

png

def plot_digits(instances, images_per_row=10, **options):
    size = 28
    images_per_row = min(len(instances), images_per_row)
    images = [instance.reshape(size,size) for instance in instances]
    n_rows = (len(instances) - 1) // images_per_row + 1
    row_images = []
    n_empty = n_rows * images_per_row - len(instances)
    images.append(np.zeros((size, size * n_empty)))
    for row in range(n_rows):
        rimages = images[row * images_per_row : (row + 1) * images_per_row]
        row_images.append(np.concatenate(rimages, axis=1))
    image = np.concatenate(row_images, axis=0)
    plt.imshow(image, cmap = matplotlib.cm.binary, **options)
    plt.axis("off")

plt.figure(figsize=(9,9))
example_images = train_set.iloc[1:21,1:].values
plot_digits(example_images, images_per_row=10)
plt.show()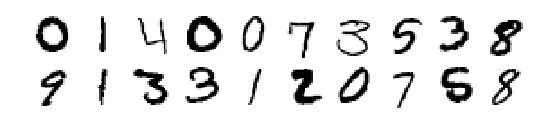

png

训练一个二分类器

首先把原有的训练集拆分成训练集和验证集
训练模型，随机验证实例效果，反应还不错的样子

from sklearn.model_selection import train_test_split
minist_train , minist_test = train_test_split(train_set, test_size = 0.2, random_state = 42)

minist_train_feature = minist_train.iloc[:,1:]
minist_train_target = minist_train.iloc[:,0]
minist_test_feature = minist_test.iloc[:,1:]
minist_test_target = minist_test.iloc[:,0]

minist_train_target_5 = (minist_train_target == 5)
minist_test_target_5 = (minist_test_target == 5)

from sklearn.linear_model import SGDClassifier
sgd_clf = SGDClassifier()
sgd_clf.fit(minist_train_feature,minist_train_target_5)

D:\Anaconda\Lib\site-packages\sklearn\linear_model\stochastic_gradient.py:144: FutureWarning: max_iter and tol parameters have been added in SGDClassifier in 0.19. If both are left unset, they default to max_iter=5 and tol=None. If tol is not None, max_iter defaults to max_iter=1000. From 0.21, default max_iter will be 1000, and default tol will be 1e-3.
      FutureWarning)
      
SGDClassifier(alpha=0.0001, average=False, class_weight=None,
	   early_stopping=False, epsilon=0.1, eta0=0.0, fit_intercept=True,
	   l1_ratio=0.15, learning_rate='optimal', loss='hinge', max_iter=None,
	   n_iter=None, n_iter_no_change=5, n_jobs=None, penalty='l2',
	   power_t=0.5, random_state=None, shuffle=True, tol=None,
	   validation_fraction=0.1, verbose=0, warm_start=False)

sgd_clf.predict(np.array(minist_test_feature.iloc[3,:]).reshape(1,-1))

array([False], dtype=bool)

print(minist_test_target.iloc[3])
plot_digit(minist_test_feature.iloc[3].values)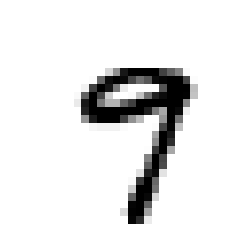

png

衡量性能

首先用交叉验证，可以看到用精度指标衡量可以说很高了

from sklearn.model_selection import cross_val_score
score = cross_val_score(sgd_clf,minist_train_feature, minist_train_target_5, cv = 3, scoring="accuracy")

score ##这里的精度指的是  预测正确的/总的预测量，由于是5的数字足够少，不是五的精度自然就高，所以这样的衡量是不准确的

array([ 0.960625  ,  0.95535714,  0.91705357])

引出混淆矩阵和分类的常见指标

混淆矩阵：A 类被分类成 B 类的次数，混淆矩阵的每一行代表一个实例，每一列代表预测的实例 [TN , FP]，[FN , TP]]
准确率：，预测为 5 中，实际也为 5 的概率
召回率：，实际是 5 中，被正确预测的概率
- 前面一个字母代表预测的结果是正确的还是错误的，T 为正确
- 后一个字母代表预测的结果，所以 TP：预测为 5，实际也为 5；FP：预测为 5，实际不为 5
F1：准确率和召回率的调和平均数 $准确率召回率$

from sklearn.model_selection import cross_val_predict ##返回的是交叉验证的预测值,它用一份训练的模型预测另外两份的数据
minist_train_5_predict = cross_val_predict(sgd_clf,minist_train_feature, minist_train_target_5, cv = 3)

from sklearn.metrics import confusion_matrix
confusion_matrix(minist_train_target_5, minist_train_5_predict)

array([[30125,   382],
	   [  957,  2136]], dtype=int64)

from sklearn.metrics import precision_score,recall_score,f1_score
print("precision_score:",precision_score(minist_train_target_5, minist_train_5_predict))
print("recall_score:",recall_score(minist_train_target_5, minist_train_5_predict))
print("f1_score:",f1_score(minist_train_target_5, minist_train_5_predict))

precision_score: 0.848292295473
recall_score: 0.690591658584
f1_score: 0.761361611121

准确率和召回率的指导意义

如果对影片进行分类，我们倾向于抵制很多好的影片（低召回率）但只对孩子友好的影片（高准确率）。而不是尽可能多的收录好的影片而使对孩子不友好的影片成为偶尔的漏网之鱼。你无法将二者兼顾，因为他们是相互矛盾的。下面给出如何权衡的方法：

这两货和决策边界有关，可以调整决策边界从而调整准确率与召回率
这里的决策边界即是 decision_function 的得分数，靠这个来决定一个实例是正还是负

minist_train_5_scores = cross_val_predict(sgd_clf,minist_train, minist_train_target_5, cv = 3,method="decision_function")

from sklearn.metrics import precision_recall_curve
precisions,recalls,thresholds = precision_recall_curve(minist_train_target_5, minist_train_5_scores)
precisions,recalls,thresholds

(array([ 0.09374432,  0.09371685,  0.09371969, ...,  1.        ,
		 1.        ,  1.        ]),
 array([  1.00000000e+00,   9.99676689e-01,   9.99676689e-01, ...,
		  6.46621403e-04,   3.23310702e-04,   0.00000000e+00]),
 array([-2236830.96022862, -2236233.25582415, -2235604.48919789, ...,
		 1842781.66629909,  1875424.58915392,  2179185.94987394]))

def plot_precision_recall_vs_threshold(precisions, recalls, thresholds):
    plt.plot(thresholds, precisions[:-1], "b--", label="Precision", linewidth=2)
    plt.plot(thresholds, recalls[:-1], "g-", label="Recall", linewidth=2)
    plt.xlabel("Threshold", fontsize=16)
    plt.legend(loc="upper left", fontsize=16)
    plt.ylim([0, 1])

plt.figure(figsize=(8, 4))
plot_precision_recall_vs_threshold(precisions, recalls, thresholds)
plt.xlim([-700000, 700000])
plt.show()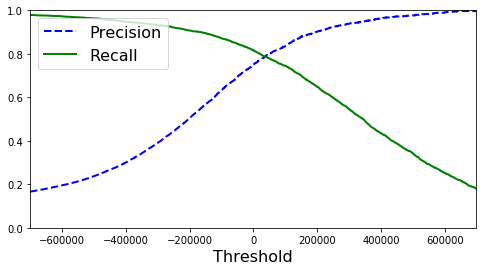

png

thresholdsh = 600000
example_digit_score = sgd_clf.decision_function(np.array(minist_test_feature.iloc[3,:]).reshape(1,-1))
example_digit_score

array([-815979.04308431])

y_score = (example_digit_score > thresholds)
y_score

array([ True,  True,  True, ..., False, False, False], dtype=bool)

ROC 曲线

TPR：在所有实际为阳性的样本中，被正确地判断为阳性之比率。
FPR：在所有实际为阴性的样本中，被错误地判断为阳性之比率。
ROC 曲线即是以 FPR 为横坐标，TPR 为纵坐标绘制的曲线。
给定一个二元分类模型和它的阈值，就能从所有样本的（阳性／阴性）真实值和预测值计算出一个 (X=FPR, Y=TPR) 座标点。

从 (0, 0) 到 (1,1) 的对角线将 ROC 空间划分为左上／右下两个区域，在这条线的以上的点代表了一个好的分类结果（胜过随机分类），而在这条线以下的点代表了差的分类结果（劣于随机分类）。

完美的预测是一个在左上角的点，在 ROC 空间座标 (0,1) 点，X=0 代表着没有伪阳性，Y=1 代表着没有伪阴性（所有的阳性都是真阳性）；也就是说，不管分类器输出结果是阳性或阴性，都是 100% 正确。一个随机的预测会得到位于从 (0, 0) 到 (1, 1) 对角线（也叫无识别率线）上的一个点；最直观的随机预测的例子就是抛硬币。

好的分类器曲线应尽可能的向左上角靠，用曲线下的面积 AUC 衡量，面积越大，分类越好

from sklearn.metrics import roc_curve
fpr, tpr, thresholds = roc_curve(minist_train_target_5,minist_train_5_scores)

def plot_roc_curve(fpr, tpr, label=None):
    plt.plot(fpr, tpr, linewidth=2, label=label)
    plt.plot([0, 1], [0, 1], 'k--')
    plt.axis([0, 1, 0, 1])
    plt.xlabel('False Positive Rate')
    plt.ylabel('True Positive Rate')

plot_roc_curve(fpr, tpr)
plt.show()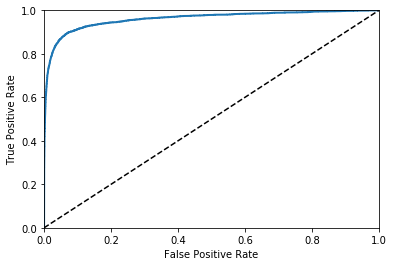

png

from sklearn.metrics import roc_auc_score
roc_auc_score(minist_train_target_5,minist_train_5_scores)

0.96090535941086852

多类别分类及算法

有一些算法直接进行多类别分类（随机森林，朴素贝叶斯），而有些只能二分类（支持向量机，线性分类）
一对所有分类：训练十个二分类器（0 的分类，1 的分类…），返回决策分数最高的即是所要的
一对一分类：训练对任意两个数字区分的模型，如果有 N 个类，意味着要训练 N(N-1)/2 个模型
直接进行多分类受制于训练集的大小，而一对一分类在多类别且小数量集上显然更快。对于大多数算法，一对多是能接受的。

some_digit = np.array(minist_test_feature.iloc[3]).reshape(1,-1)

sgd_clf.fit(minist_train_feature , minist_train_target)

D:\Anaconda\Lib\site-packages\sklearn\linear_model\stochastic_gradient.py:144: FutureWarning: max_iter and tol parameters have been added in SGDClassifier in 0.19. If both are left unset, they default to max_iter=5 and tol=None. If tol is not None, max_iter defaults to max_iter=1000. From 0.21, default max_iter will be 1000, and default tol will be 1e-3.
  FutureWarning)

SGDClassifier(alpha=0.0001, average=False, class_weight=None,
	   early_stopping=False, epsilon=0.1, eta0=0.0, fit_intercept=True,
	   l1_ratio=0.15, learning_rate='optimal', loss='hinge', max_iter=None,
	   n_iter=None, n_iter_no_change=5, n_jobs=None, penalty='l2',
	   power_t=0.5, random_state=None, shuffle=True, tol=None,
	   validation_fraction=0.1, verbose=0, warm_start=False)

sgd_clf.predict(some_digit)

array([9], dtype=int64)

some_digit_scores = sgd_clf.decision_function(some_digit)
some_digit_scores

array([[ -920353.27712984, -1279235.87154285, -1366480.72646492,
		 -595927.50279798,  -482684.25204249,  -683359.55644181,
		-1087498.56196379,  -225410.75309   ,  -501095.68715396,
		  181111.64068788]])

np.argmax(some_digit_scores) ##9

sgd_clf.classes_        ##这里的类别是它按大小排的

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9], dtype=int64)

一对一以及一对多策略

如果想要 sklearn 用一对一，一对多，进行下列操作
当然，这只针对只能训练二分类器的算法

from sklearn.multiclass import OneVsOneClassifier
ovo_clf = OneVsOneClassifier(SGDClassifier(random_state=42))
ovo_clf.fit(minist_train_feature , minist_train_target)
ovo_clf.predict(some_digit)

len(ovo_clf.estimators_)  ##很显然，训练了45个二分类器

##我们也可以直接用随机森林多分类
from sklearn.ensemble import RandomForestClassifier
forest_clf = RandomForestClassifier(random_state=42)
forest_clf.fit(minist_train_feature , minist_train_target)
forest_clf.predict(some_digit)

D:\Anaconda\Lib\site-packages\sklearn\ensemble\forest.py:248: FutureWarning: The default value of n_estimators will change from 10 in version 0.20 to 100 in 0.22.
  "10 in version 0.20 to 100 in 0.22.", FutureWarning)

array([9], dtype=int64)

forest_clf.predict_proba(some_digit)

array([[ 0.1,  0. ,  0. ,  0. ,  0.1,  0. ,  0. ,  0.1,  0. ,  0.7]])

误差分析

混淆矩阵及其可视化
由于正则化能显著提升随机梯度下降算法的性能，这里用一下

from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
minist_train_feature_scaler = scaler.fit_transform(minist_train_feature)
minist_train_feature_scaler

D:\Anaconda\Lib\site-packages\sklearn\preprocessing\data.py:617: DataConversionWarning: Data with input dtype int64 were all converted to float64 by StandardScaler.
  return self.partial_fit(X, y)
D:\Anaconda\Lib\site-packages\sklearn\base.py:462: DataConversionWarning: Data with input dtype int64 were all converted to float64 by StandardScaler.
  return self.fit(X, **fit_params).transform(X)

array([[ 0.,  0.,  0., ...,  0.,  0.,  0.],
	   [ 0.,  0.,  0., ...,  0.,  0.,  0.],
	   [ 0.,  0.,  0., ...,  0.,  0.,  0.],
	   ...,
	   [ 0.,  0.,  0., ...,  0.,  0.,  0.],
	   [ 0.,  0.,  0., ...,  0.,  0.,  0.],
	   [ 0.,  0.,  0., ...,  0.,  0.,  0.]])

minist_train_pred = cross_val_predict(sgd_clf,minist_train_feature_scaler,minist_train_target,cv=3)

conf_mx = confusion_matrix(minist_train_target,minist_train_pred)
conf_mx

array([[3214, 1, 10, 11, 4, 25, 32, 4, 14, 1],
   [   0, 3633,   24,   16,    1,   24,    7,    6,   60,    4],
   [  29,   18, 2960,   64,   53,   21,   44,   41,   87,   14],
   [  24,   26,   76, 2997,    4,  122,   26,   22,   71,   46],
   [  12,   23,   28,    5, 2955,    4,   28,   14,   39,  125],
   [  49,   30,   16,  109,   40, 2615,   64,   21,   91,   58],
   [  27,   11,   28,    0,   20,   50, 3193,    2,   21,    0],
   [  18,   14,   45,   14,   17,    7,    4, 3251,    9,  129],
   [  32,   87,   30,  110,    7,   95,   27,   17, 2742,   81],
   [  29,   19,   18,   51,  106,   16,    0,  120,   48, 2943]], dtype=int64)

plt.matshow(conf_mx, cmap=plt.cm.gray)
plt.show()

png

可以看到上图的主对角线很白，说明分类良好，其他地方有比较明显的暗斑，说明存在着比较大的分类错误

然而我们不应该着眼于绝对数值，而是衡量误差，与此对应的是将每个方框出现的比例按颜色深浅绘成图形，这样，颜色越白的地方分类产生的误差越大。

这样就能针对性的提升模型的性能，比如多收集某些数据，加强某些数字的区分

row_sums = conf_mx.sum(axis=1, keepdims=True)
norm_conf_mx = conf_mx / row_sums

np.fill_diagonal(norm_conf_mx, 0)
plt.matshow(norm_conf_mx, cmap=plt.cm.gray)
plt.show()

png